
Особое внимание было уделено влиянию распыляемой воды в первой и второй камерах цементной мельницы соответственно на процессы гидратации и дегидратации гипса и, в конечном итоге, на свойства цемента. Была также сделана оценка влияния интенсификатора помола на тонкость помола известнякового наполнителя. 1 Анализ чувствительности Основываясь на работе [1], можно выразить суть анализа чувствительности в способности описывать сложные статистические модели в отношении того, в какой степени и в каком направлении Х-переменная или группа Х-переменных вместе влияют на Y. В такой же форме анализ чувствительности был применен в работе Свиннинга и др. [2]. В [2] анализ чувствительности определяется, как проверка предсказанного влияния Х-переменной или латентной переменной на Y-переменную отклика в пределах доверительной области предсказанной Y. Кроме то го, может быть также произведена проверка неопределенности коэффициентами регрессии. Мартенс и Мартенс [3] разработали усовершенствованный метод проверки неопределенности, основанный на перекрестной проверке, расщеплении выборки и диаграмме устойчивости. Этот метод был включен в качестве приложения к программному пакету Unscrambler® версии 7.5. Основываясь на примерах регрессионных моделей PLS, описанных в [1], корреляцию переменных Х и Y можно оценивать различными путями: Цементный завод в Бревике компании Norcem A.S. Dalen – сравнение коэффициентов регрессии различных переменных PLS с центрированными и нормированными данными; – проверка достоверности коэффициентов методом расщепления выборки с доверительным интервалом 0,95. На рис. 1 коэффициенты регрессии (вертикальные оси) для предсказания свойств цемента по переменным (горизонтальные оси), описывающим условия процесса в цементной мельнице, показаны для водоцементного отношения, необходимого для достижения нормальной густоты (а), срока схватывания (b) и однодневной прочности при сжатии (с). Количество осей Х соответствует списку переменных в таблице 2 части 1 данной работы [1]. Предсказание отклонения по Y, включая доверительную область, равную делается по отклонению одной Х-переменной, равными шагами, при условии, что другие Х-переменные остаются постоянными и равными своим средним значениям соответственно. Область отклонения в данной работе ограничена следующим образом: xk ± 1,5s(xk). 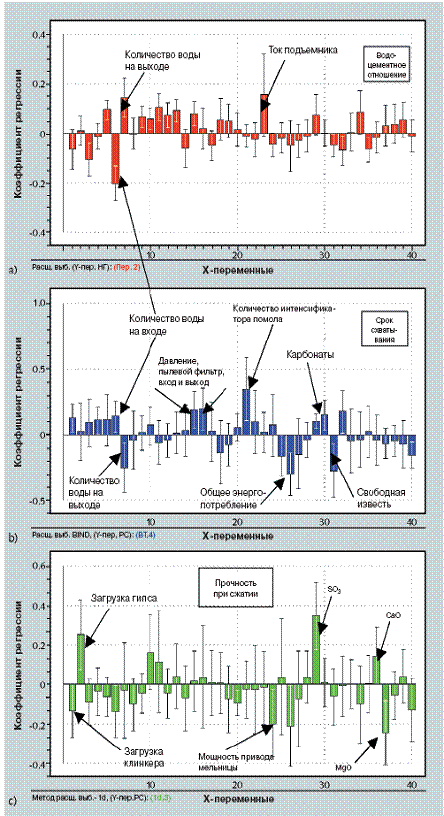
1 Коэффициенты регрессии Примеры даны на рис. 2 и 3. Предсказание отклонения переменной по Y является результатом изменения одной латентной переменной от одного наблюденного экстремума до другого. Вычисление отклонения по Δxk в оригинальной не нормированной форме производится варьированием А-той латентной переменной Δt pa, следующим образом: Δxk = (Δt pkа) s(xk) (1) Аналогично предыдущему анализу чувствительности с изменением только одной Х-переменной, множество t варьируется в одном направлении с шагом Δt. Пример, в котором продемонстрировано вычисление значений Δх, показан на рис. 4. Вычисление Х в нецентрированном и ненормированном виде происходит тогда следующим образом: xk = (t pka ) s(xk) + x̄k (2) В этих двух типах анализа чувствительности искусственное наблюдение Х-матрицы было проведено до предсказания. В первом случае исследуемая по фактору влияния переменная изменялась пошагово в течение пяти шагов, что дало шесть наблюдений в данном интервале отклонений, в то время как другие переменные оставались постоянными. В случае изменения латентной переменной, пошаговому изменению подвергались все переменные в течение 5 шагов. В качестве альтернативного варианта могло бы стать искусственное наблюдение Х-матрицы, содержащей выборку Х-переменных, которые изменяются равными шагами при условии, что остальные переменные остаются постоянными и равными своим средним значениям. Характер изменений может быть определен при помощи главных компонентов или латентных переменных по анализу главных компонентов (PCA) этих переменных. Корреляция Х - и Y-переменных, рассматриваемых в данной работе, была бы достаточно высокой, если бы не перекрывание доверительной области ŷ±s(y) предсказанными максимумами и минимумами Y, соответственно. По оценке значимости влияния переменной xk по методу расщепления выборки, влияние можно считать значимым, если уровень неопределенности не превышает 2 |bwk|.
|
