В статье проводится анализ чувствительности путем прогнозирования смоделированных отклонений единичных Х-переменных и латентных переменных.

Особое внимание было уделено влиянию распыляемой воды в первой и второй камерах цементной мельницы соответственно на процессы гидратации и дегидратации гипса и, в конечном итоге, на свойства цемента. Была также сделана оценка влияния интенсификатора помола на тонкость помола известнякового наполнителя.

1 Анализ чувствительности

Основываясь на работе [1], можно выразить суть анализа чувствительности в способности описывать сложные статистические модели в отношении того, в какой степени и в каком направлении Х-переменная или группа Х-переменных вместе влияют на Y. В такой же форме анализ чувствительности был применен в работе Свиннинга и др. [2]. В [2] анализ чувствительности определяется, как проверка предсказанного влияния Х-переменной или латентной переменной на Y-переменную отклика в пределах доверительной области предсказанной Y. Кроме то го, может быть также произведена проверка неопределенности коэффициентами регрессии. Мартенс и Мартенс [3] разработали усовершенствованный метод проверки неопределенности, основанный на перекрестной проверке, расщеплении выборки и диаграмме устойчивости. Этот метод был включен в качестве приложения к программному пакету Unscrambler® версии 7.5.

Основываясь на примерах регрессионных моделей PLS, описанных в [1], корреляцию переменных Х и Y можно оценивать различными путями: Цементный завод в Бревике компании Norcem A.S. Dalen – сравнение коэффициентов регрессии различных переменных PLS с центрированными и нормированными данными; – проверка достоверности коэффициентов методом расщепления выборки с доверительным интервалом 0,95. На рис. 1 коэффициенты регрессии (вертикальные оси) для предсказания свойств цемента по переменным (горизонтальные оси), описывающим условия процесса в цементной мельнице, показаны для водоцементного отношения, необходимого для достижения нормальной густоты (а), срока схватывания (b) и однодневной прочности при сжатии (с). Количество осей Х соответствует списку переменных в таблице 2 части 1 данной работы [1]. Предсказание отклонения по Y, включая доверительную область, равную делается по отклонению одной Х-переменной, равными шагами, при условии, что другие Х-переменные остаются постоянными и равными своим средним значениям соответственно. Область отклонения в данной работе ограничена следующим образом: xk ± 1,5s(xk).

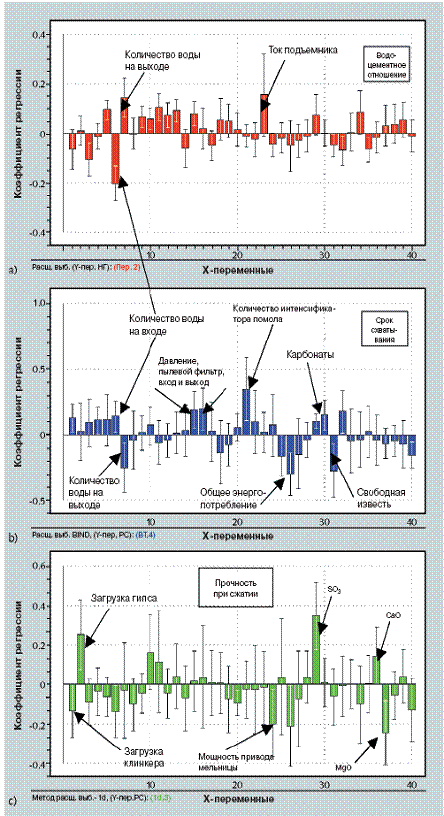
1 Коэффициенты регрессии

Примеры даны на рис. 2 и 3. Предсказание отклонения переменной по Y является результатом изменения одной латентной переменной от одного наблюденного экстремума до другого. Вычисление отклонения по Δxk в оригинальной не нормированной форме производится варьированием А-той латентной переменной Δt pa, следующим образом: Δxk = (Δt pkа) s(xk) (1) Аналогично предыдущему анализу чувствительности с изменением только одной Х-переменной, множество t варьируется в одном направлении с шагом Δt. Пример, в котором продемонстрировано вычисление значений Δх, показан на рис. 4. Вычисление Х в нецентрированном и ненормированном виде происходит тогда следующим образом: xk = (t pka ) s(xk) + x̄k (2) В этих двух типах анализа чувствительности искусственное наблюдение Х-матрицы было проведено до предсказания. В первом случае исследуемая по фактору влияния переменная изменялась пошагово в течение пяти шагов, что дало шесть наблюдений в данном интервале отклонений, в то время как другие переменные оставались постоянными. В случае изменения латентной переменной, пошаговому изменению подвергались все переменные в течение 5 шагов. В качестве альтернативного варианта могло бы стать искусственное наблюдение Х-матрицы, содержащей выборку Х-переменных, которые изменяются равными шагами при условии, что остальные переменные остаются постоянными и равными своим средним значениям. Характер изменений может быть определен при помощи главных компонентов или латентных переменных по анализу главных компонентов (PCA) этих переменных. Корреляция Х - и Y-переменных, рассматриваемых в данной работе, была бы достаточно высокой, если бы не перекрывание доверительной области ŷ±s(y) предсказанными максимумами и минимумами Y, соответственно. По оценке значимости влияния переменной xk по методу расщепления выборки, влияние можно считать значимым, если уровень неопределенности не превышает 2 |bwk|.

2 Предсказание свойств цемента

2.1 База: условия процесса в цементной мельнице. На рис. 1 видно, как, анализируя размер, направление (позитивное или негативное влияние) и неопределенность соответствующих коэффициентов bwk, можно оценить влияние каждой переменной процесса Xj, включенной в регрессию PLS, на три основных свойства цемента. Все переменные, представленные на рис. 1, перечислены в табл. 2, в части первой [1] данной работы. Примеры предсказаний отклонений в свойствах цемента по одной изменяемой Х-переменной при условии, когда остальные переменные остаются постоянными и равными своим средним значениям, представлены на рис. 2 и 3. В качестве примера влияния латентной переменной на Y-переменную на рис. 4 показано изменение водоцементного отношения, необходимого для достижения нормальной густоты, предсказанного по отклонению латентной переменной №1.  Все переменные, отображенные на рис. 1, которые имеют основное и значимое влияние на свойства цемента, представлены ниже (положительное и отрицательное влияние отмечено знаками + и – соответственно).

Водоцементное отношение, необходимое для достижения нормальной густоты: – загрузка сульфата двухвалентного железа (–), – количество распыляемой воды на входе мельницы (–), – количество распыляемой воды на выходе мельницы (+), – скорость ротора классификатора (+), – возврат материала в классификатор (+). Срок схватывания:
– количество распыляемой воды на входе мельницы (+),  – количество интенсификатора помола (+), – количество карбонатов (+), – количество распыляемой воды на выходе мельницы (–), – общее электропотребление (–), – количество свободной извести (–), – температура клинкера при загрузке в цементную мельницу (–). Однодневная прочность при сжатии:  – загрузка клинкера (–), – загрузка гипса (+), – количество SO3 (+),– количество CaO (+), – мощность привода мельницы (–).

Как показал Ли [4], однодневная прочность при сжатии значительно возрастает при возрастании содержания SO3. Тот факт, что прочность также значительно растет при возрастании содержания гипса, свидетельствует о том, что S03 оказывает влияние на прочность независимо от формы, в которой он поступает, либо в составе гипса, либо в составе клинкера. Отсутствие влияния гипса на срок схватывания может быть объяснено (см. Ли [4] и рис. 3, ч. 1 [1] данной работы) изменениями степени дегидратации гипса. Рис. 3 демонстрирует значительное увеличение срока схватывания с возрастанием количества интенсификатора помола. Возможные причины этого влияния будут обсуждены ниже, в следующей главе. На рис. 1 отображены две переменные процесса: количество воды распыляемой на входе и выходе мельницы, соответственно, влияет, как на срок схватывания, так и на водоцементное отношение, необходимое для достижения нормальной густоты (НГ). Слегка обескураживает уменьшение срока схватывания при возрастании значения второй переменной процесса. Эксперименты, проводимые ранее [5], приводили к обратному результату: вода, независимо от места распыления в мельнице, способствовала прегидратации минералов, входящих в состав клинкера. Моделирование более реалистичных отклонений Х должны быть основаны на изменениях латентных переменных.

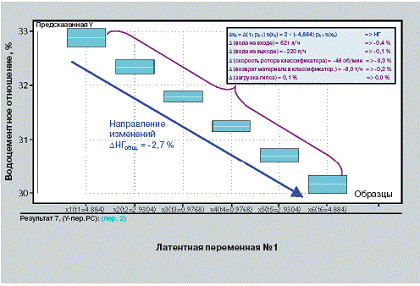
На рис. 4 показано, что изменения латентной переменной №1 ведет к значительному снижению НГ, оно дает повышение всего количества воды при понижении количества воды на выходе мельницы. Автокорреляция двух переменных объясняется тем, как осуществляется управление процессом и постановка эксперимента. Автокорреляция верифицируется первой компонентой регрессии PLS, которая влияет на объяснение главной части отклонения Y. В экспериментах с изменением количества воды, распыляемой в первой камере, заданное значение температуры цемента на выходе мельницы сохранялось постоянным. Это соответствовало обычной практике управления процессом на данном заводе. Как возврат материала, так и уровень загрузки мельницы колеблются при почти постоянном уровне загрузки клинкера, когда латентная переменная №1 изменяется в сторону отрицательной Δ НГ. Это означает, что вода, распыляемая в первой камере, делает процесс помола более эффективным, благодаря повышению эффективности процесса классификации, что, в свою очередь, можно объяснить уменьшением степени агломерации. Укороченное время пребывания в мельнице в сочетании с вероятной пониженной максимальной температурой и более высоким парциальным давлением H2O может привести к пониженной степени дегидратации гипса. По Морку [6], в результате конверсии гипса в (CaSO₂ - 0,5 H₂O) ухудшается начальные вязкостные свойства и водоцементное отношение, необходимое для достижения нормальной густоты может повыситься. Это может быть подтверждено исследованием цемента при помощи анализов ТГА и ДТГА.

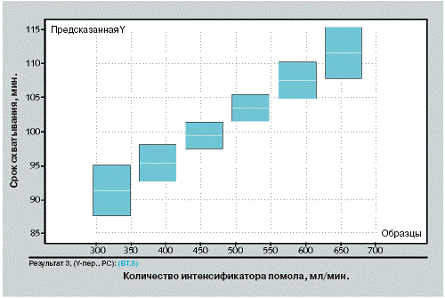
2 Предсказание изменений срока схватывания

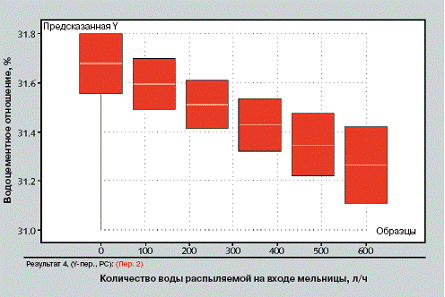
3 Предсказанные изменения водоцементного отношения, необходимого для достижения нормальной густоты

5 Предсказанные изменения в поверхностной микроструктуре (по ДТГА)

4 Предсказанные изменения водоцементного отношения, необходимого для достижения нормальной густоты

Сравнивая рис. 3 и 4, можно видеть, что доверительная область в случае предсказания изменения Y по изменениям латентной переменной гораздо меньше, чем в случае предсказания по изменению единичной X-переменной. Применимость регрессии PLS  относится к существованию главных направлений в изменениях Х-матрицы наблюдений. Латентная переменная изменяется в пределах пространства Rn при n=2 для данной модели. Пределы изменения единичной х-переменной x̄k по xk +1,5s(xk), скорее всего, находятся вне пространства R2, поэтому смоделированные изменения должны считаться менее реалистичными. Свиннингом и др. [7] разработан метод оптимизации, основанный на изменениях, ограниченных пространством Rn. 2.2 Основа: микроструктура цемента

При изучении корреляции между свойствами цемента и условиями производственного процесса с упором на микроструктуру цемента предсказания делались в двухступенчатом режиме. В течение первого шага предсказывалось изменение части микроструктуры по изменению одной (или комбинации нескольких) латентной переменной Х-матрицы наблюдений процесса. В течение следующего шага  предсказывалось изменение одного или нескольких свойств цемента по предсказанному изменению выбранной части микроструктуры. Как было упомянуто в главе 2.1, при изменении условий процесса, изменения водоцементного отношения, необходимого для достижения нормальнойгустоты (НГ) и срока схватывания (СС) можно объяснить степенью дегидратации гипса. Для моделирования влияния степени дегидратации гипса была выбрана только комбинация латентных переменных №1 и №2 , что дало Δ (загрузки гипса) ≈ 0.

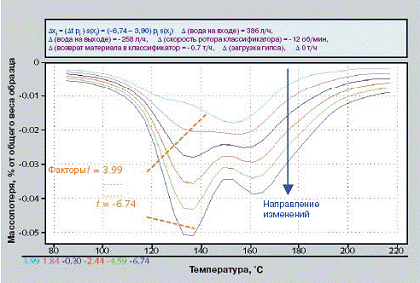
На рис. 5 показаны изменения поверхностной микроструктуры, описываемые массопотерей на каждые 4° C по ТГА в температурном интервале 85–217° C, предсказанные по изменениям латентных переменных tp1+2 = t(0,61p1 + 0,38p2). Однако в этом температурном интервале была также отмечена массопотеря от дегидратации прегидратированных минералов в составе клинкера. Повышение массопотери в области температур около 217°C вероятно означает среднее повышение прегидратации с увеличением количества воды, распыляемой в первой камере. Сравнивая корреляцию последней латентной переменной на рис. 5 и переменных на рис. 4 с изменениями некоторых Х-переменных, легко заметить, что латентные переменные не совсем идентичны. Однако результаты, отображенные на рис. 5, подтверждают предположение, высказанное в главе 2.1, о возможной корреляции между условиями процесса и степенью дегидратации гипса. Повышение количества воды, распыляемой в первой камере цементной мельницы и одновременное снижение количества воды, распыляемой в последней камере, снижает конверсию гипса в (CaSO₂•1/2H₂O). В дальнейшем, см. рис. 6, это приведет к значительному снижению НГ. А заметное увеличение показателя СС, как показано на рис. 7, может произойти частично, благодаря прегидратации минералов, входящих в состав клинкера.

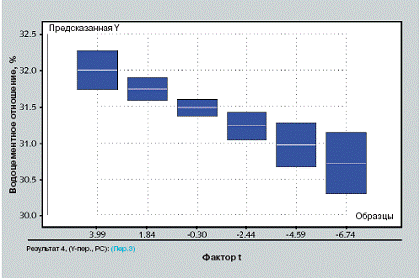
6 Предсказанные изменения водоцементного отношения, не-обходимого для достижения нормальной густоты (ср. рис. 5)

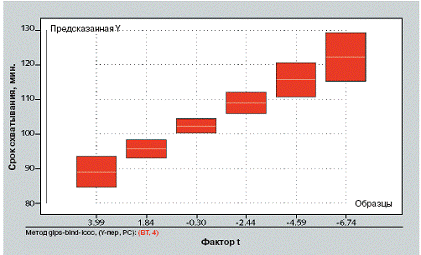
7 Предсказанные изменения срока схватывания (ср. рис. 5)

Изучая поведение кривой ДТГА в температурном интервале 604–946° C на рис. 3 ч. 1 данной работы [1], можно наблюдать отчетливое изменение положения пика кривой, указывающее на декарбонизацию известнякового наполнителя. Причина такого изменения может крыться в тонкости помола известнякового наполнителя. В печь подается известняк довольно тонкого помола, предположительно – даже более тонкого, чем клинкер, поскольку он перемалывается в мельнице. Считая, что реакция  декарбонизации во время проведения ТГА гетерогенна и проходит под диффузным контролем, температура при максимальной скорости реакции, вероятно, возрастет с уменьшением тонкости помола цементного наполнителя. Для объяснения возможных изменений тонкости помола известнякового наполнителя были изучены коэффициенты регрессии модели PLS, предназначенной для предсказания кривой ДТГА в актуальном температурном интервале по переменным процесса. Коэффициенты регрессии некоторых переменных, которые оказывают основное влияние на кривую или термограмму, представлены на рис. 8.

Кривые коэффициентов показывают, что изменение количества интенсификатора помола дает изменение положения пика. Изменение величины загрузки известнякового наполнителя приводит к изменению условий процесса, но путем варьирования латентной переменной №2 можно добиться сохранения величины загрузки известнякового наполнителя постоянной. Предсказанные изменения кривых ДТГА по изменениям латентных переменных показаны на рис. 9. Изменение положения пика с изменением показателя загрузки интенсификатора помола очевидно. Более крупная фракция известнякового наполнителя в конечном продукте объясняется тенденцией уменьшения агломерационных процессов в цементной мельнице. Изменения срока схватывания, предсказанное по изменениям поверхностной микроструктуры, отраженное на рис. 9, показано на рис. 10. Влияние этих изменений совершенно незначительно. Следовательно, дальнейшие исследования следует сфокусировать на других характеристиках микроструктуры для изучения вопроса значительного влияния интенсификатора помола на срок схватывания.

Заключение

Анализ чувствительности, проведенный путем предсказания свойств цемента и микроструктуры цемента по условиям процесса в цементной мельнице, дал следующие результаты: – выявлена высокая. Степень корреляции между количеством воды, распыляемой в первой и второй камерах цементной мельницы соответственно, степенью дегидратации гипса и двумя свойствами – водоцементным отношением, необходимым для достижения нормальной густоты и сроком схватывания; – интенсификатор помола оказывает значительное влияние на тонкость помола известнякового наполнителя; – значительные изменения срока схватывания в зависимости от изменения количества интенсификатора помола не могут быть объяснены изменением тонкости помола известнякового наполнителя.

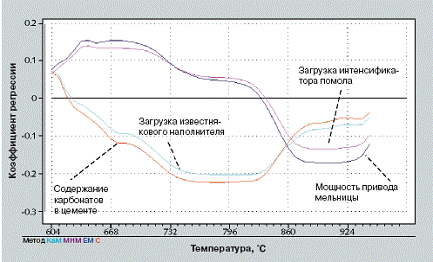
8 Коэффициенты регрессии четырех переменных процесса (часть Bw)

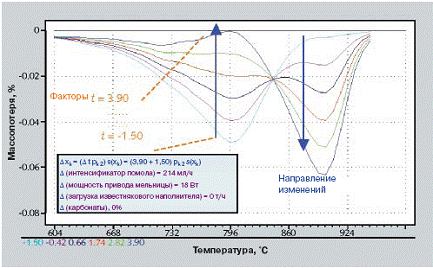
9 Предсказанные изменения поверхностной инфраструктуры (по ДТГА)

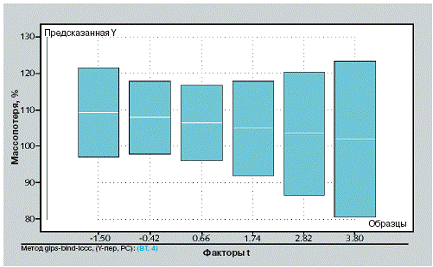
10 Предсказанные изменения срока схватывания (ср. рис. 9)

С рынком и технологическим оснащением производства ССС Вы можете познакомиться в работах Академии Конъюнктуры Промышленных Рынков:

Анализ производителей сухих строительных смесей

Анализ оборудования для производства сухих строительных смесей

Анализ оборудования для производства гипсового и ангидритового вяжущего

Анализ оборудования для сушки и фракционирования песка на фракции: 0,00- 0, 315 мм; 0,315- 0,63 мм; 0,63- 1,25 мм; 1,25- 2,5 мм.

Анализ оборудования для дробления и просеивания гидратной извести, минерального порошка, керамзитного щебня, известняковой муки  

Цемент. Известь. Гипс