Напряжение Мы уже дали разъяснения по двум или трем факторам в нашей модели. Теперь все, что нам осталось сделать, это определить напряжение. Как только мы определим напряжение, мы сможем преобразовать расчет кажущегося модуля в расчет деформации. Так, например, если мы прикладываем напряжение в 12.1 МПa (1755 фунтов на кв. дюйм), мы получим начальное напряжение в 0.1%. Через 10 часов оно повысится до 0.2%. Через 1000 часов это будет уже 0.4%, а через 10,000 часов это будет уже 0.5%. Нам известно, что у всех материалов имеется лимитирующая деформация, за пределами которой они либо становятся текучими, либо разрушаются. В случае использования очень жесткого материала, такого как композит со стекловолокном, характер разрушения будет хрупким, и избыточная деформация приведет к растрескиванию. Если бы пластмассовые материалы были идеально эластичными, все, что нам понадобилось бы сделать, так это просто измерить предельную деформацию, и мы смогли бы легко рассчитать ожидаемое время до отказа для каждого данного напряжения. Следует избегать напряжений, которые могут вызывать прогнозируемые отказы до истечения желательного срока эксплуатации продукта. К сожалению, у пластмассовых материалов не бывает идеально эластичного поведения на протяжении всей кривой «напряжения – деформации». Как мы продемонстрировали в части, опубликованной в прошлом месяце, линейно упругое поведение, можно получить для сравнительно небольшой части кривой «напряжения – деформации» до точки, известной как предел упругой деформации. (Заметим вскользь, что предел упругой деформации материала это параметр, который очень полезно иметь в перечне данных. Но не стоит надрываться, отыскивая эти данные, поставщики материалов их не предоставляют). После того, как напряжения достаточно высоки для того, чтобы превысить предел упругой деформации, применение следующего приращения напряжения приводит к деформации большей, нежели можно ожидать при идеальном эластичном поведении. По этой причине нам необходимо иметь кривую «напряжения – деформации» для материала. И нам не может быть достаточно кривой «напряжения – деформации» при комнатной температуре; она должна быть сгенерирована при той же температуре, что и та, которую мы используем для моделирования поведения ползучести. До тех пор, пока прогнозируемая обобщенная кривая деформации от ползучести будет оставаться на уровне или ниже предела упругой деформации, мы можем использовать данные, вычисленные непосредственно из уравнения для Ea. Как только прогнозируемая деформация превысит предел упругой деформации, мы должны будет внести коррективы в расчет, эмпирически используя реальные значения с кривой «напряжения – деформации».
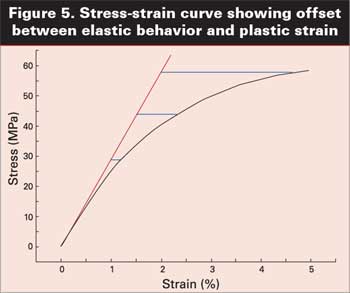
На Рисунке 5 представлен пример этого перехода от прогнозируемого линейного поведения к реальному отклику. Это кривая «напряжения – деформации» при комнатной температуре для ненаполненного ацеталевого сополимера, но принцип один и тот же для любого материала. Линия модуля показывает отклонение кривой от идеально упругого поведения (красная линии). По мере того, как прогнозируемая деформация с обобщенной кривой становится все больше, поправочный коэффициент становится больше, поскольку материал отклоняется от линейного поведения под все более возрастающим углом. При прогнозируемой 1% деформации реальная деформация составляет примерно 1.2%. Но при прогнозируемой деформации в 1.5% реальная деформация составляет примерно 2.3%. А при прогнозируемой деформации в 2% реальная деформация будет в два раза выше прогнозируемой при 4.65%. У нас есть технология Итак, мы рассмотрели все три фактора, которые определяют поведение ползучести материала: температуру, время и напряжение. Используя эти инструменты, мы можем дать ответы на трудные вопросы о поведении материала при практически любых условиях постоянных нагрузок, которые только можно вообразить, и это можно осуществлять в пределах разумных временных рамок всего за небольшую часть затрат на испытания в режиме реального времени. В нашем последнем выпуске мы проиллюстрируем использование этих инструментов при выборе материала для двух применений, используемых на очень различных рынках. В одном случае анализ позволил избежать использования материала, который был дешевле, но вызвал бы отказ. В другом случае анализ показал, что можно использовать материал, который обходится дешевле, чем изначально выбранный для этого применения. Newchemistry.ru |
