Эта серия статей предназначена для того, чтобы помочь формовщикам понять, как некоторые аналитические инструменты могут помочь в диагностике причин  брака при изготовлении детали.

Как уже отмечалось в двух предшествующих статьях, на механическое поведение пластмассовых материалов оказывают воздействие сочетания таких факторов, как температура, время и напряжение. При оценке долговременных реакций, таких как ползучесть, релаксация напряжения или утомление материала, необходимо рассматривать все три фактора как единое целое. Их нельзя рассматривать в вакууме, и если какой-либо из них изменится, необходимо производить переоценку расчетов пригодности к использованию данного материала.

В данной статье мы рассмотрим значимость явления ползучести и методы осуществления оценки долговременного поведения с использованием испытаний, которые сокращают временные рамки с лет до недель или даже дней.

Любой материал, при применении к нему напряжения, дает определенный вид деформации или напряжения. Отношение напряжения к деформации известно как модуль данного материала, и считается мерой жесткости материала. Математически это соотношение выражается как:

E = s/e

где E - это модуль, s - это напряжение, а e - это деформация. (Ученые используют в своих уравнениях множество греческих букв для того, чтобы показать себя более знающими и отпугивать непрофессионалов). Жесткий материал в больше степени противостоит деформации, а это дает более высокий расчетный модель.

В пластмассе привнесенное напряжение сохраняется на протяжении определенного периода времени, затем деформация усилится по сравнению с исходным значением, которое было при изначальном привнесении напряжения. Такая дополнительная деформация известна как напряжение ползучести, а поведение выражается модифицированным видом того же самого уравнения:

Ea = st/(eo+ec)

где ec - это деформация ползучести, а eo обозначает исходную деформацию, которую имеет деталь при привнесении напряжения. Срок действия напряжения (st) постоянный, и теперь имеется значение продолжительности (t = время).

Дополнительная деформация из-за ползучести увеличивает знаменатель данного уравнения, в то время как числитель остается без изменений. Это дает, в результате, уменьшение рассчитанного модуля, который обозначается нижним индексом “a” и называется предполагаемым модулем, поскольку вычисления предполагают, что жесткость материала уменьшается. Тем не менее, жесткость материала на самом деле не уменьшается; Ea – это математический конструкт для иллюстрации воздействия ползучести. Если нам известно поведение Ea на протяжении определенного периода времени, мы можем рассчитать  деформацию ползучести в любой заданный момент времени за счет введения различных значений напряжения.

Температура

Было время, когда исследователи полимеров потратили много усилий на измерение долговременного поведения пластмассовых материалов, В литературе можно все еще отыскать результаты этих исследований, если, конечно, искать очень усердно. Но, похоже, что, по большей части, мы ограничиваемся только просмотром перечней данных, которые ничего не говорят о долговременном поведении, и не отражают результатов воздействия температуры на пластмассовый материал.

Это очень расстраивает (или должно очень расстраивать) инженеров-проектировщиков, которые пытаются выбрать подходящий материал для конкретного применения, и это серьезное препятствие на пути процесса от производства из металла к производству из пластмассы. Представьте себе, что можно сказать инженеру, что свойства материала изменяются при повышении температуры, и не иметь при этом никаких количественных данных для того, чтобы ответить на вопрос о том, какова степень этих изменений.

И дело не в том, что неизвестно, откуда взять ответ на этот вопрос. Можно оснастить любую разрывную испытательную машину камерой искусственного климата, и осуществлять испытания образцов при самых различных температурах для получения необходимых кривых «напряжения – деформации». Можно провести динамомеханический анализ (DMA) материала для получения большого объема информации о поведении материала в зависимости от температуры.

Так, например на Рисунке1 дается график зависимости модуля упругости от температуры для 33% армированного стекловолокном PA 66. Используя эту кривую, инженер может определить жесткость материала в любой точке между комнатной температурой и точкой плавления. А вместо этого, инженерному сообществу обычно предоставляется только температура прогиба под нагрузкой, параметр, бесполезность и несущественность которого находятся за гранью разумного.

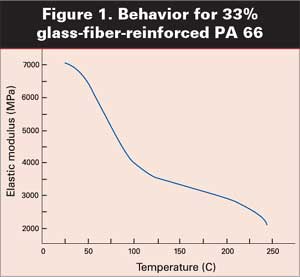
Время

Но недостаточно знать только влияние температурного фактора. У нас должен быть какой-то способ фиксирования воздействия и времени, и напряжения. Основной отговоркой для того, чтобы не проводить долговременные оценки, такие как испытания на ползучесть, является то, что в нашем мире, с его дефицитом времени, просто не хватает времени для таких вещей.  Хорошими новостями является то, что, когда дело доходит до явлений релаксации, таких как релаксация ползучести, мы можем регулировать соотношение между температурой и временем для того, чтобы быстро получить очень хорошую оценку долговременного воздействия длительного нагружения при практически любых условиях, которые мы захотим определить.

Для того, чтобы сделать это, мы опирается на принцип, который гласит, что одни и те же процессы релаксации, которые протекают быстро при повышенных температурах, будут иметь место и при пониженных температурах, но будет происходить несколько медленнее. Если мы можем экспериментальным путем установить количественное соотношение между временем и температурой, мы можем использовать результаты кратковременных испытаний для создания прогноза относительно долговременного поведения.

На Рисунке 2 приведены результаты серии кратковременных испытаний ползучести, проведенных на винильном эфирном композите, наполненном стекловолокном при температурах в диапазоне от 100°C до 135°C с повышением  температуры на 5 градусов C. Данные для каждого такого повышения температуры даются в виде логарифмической кривой для Ea как функции времени. Мы можем использовать метод, известный как метод создания температурно-временной суперпозиции, для разработки того, что известно как обобщенная кривая зависимости Ea и времени для каждого данного значения температуры.

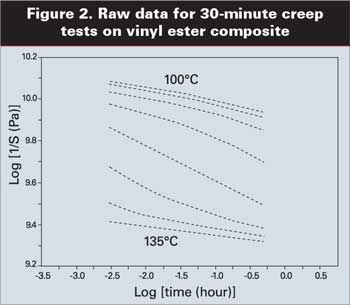
Это делается следующим образом: выбирается нужная нам температура, которая называется сопоставительной температурой. Остальные множества данных перемещаются до тех пор, пока они не будут находиться на той же самой линии, что и множество точек, описанных сопоставительной температурой. Множества данных, генерированных при температурах выше сопоставительной температуры, перемещаются вправо, в то время как, множества данных, созданных при более низких температурах, перемещаются влево. Поскольку нас, в первую очередь, интересует прогноз на будущее, мы, скорее всего, выберем самую низкую температуру из множества данных, и будем перемещать все остальные данные вправо в область более продолжительных временных рамок.

На Рисунке 3 представлена обобщающая кривая для данного создаваемого процесса. Некоторые множества данных уже перемещены, и кривая уже начинает приобретать соответствующую форму, но все еще не получилось ничего особенно интересного, поскольку мы еще не воспользовались всеми имеющимися в нашем распоряжении данными. Кривая к данной точке распространяется всего лишь на 30 часов, а это не очень хороший результат для данных, на создание которых, возможно, было истрачено до 16 часов.

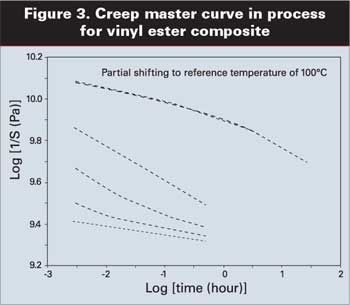
Тем не менее, за счет использования дополнительных данных, полученных при более высоких температурах, мы можем получить окончательную обобщающую кривую, которая представлена на Рисунке 4. Вот здесь уже имеется кое-что интересное. Испытание, на проведение которого затратили 16 часов, позволило сделать прогноз поведения на период, превышающий 100,000 часов или более чем на 11.5 лет. Снабженные комментариями значения на кривой позволяют нам прочитать данные с логарифмической кривой, и дают нам ценную количественную информацию об этом материале.

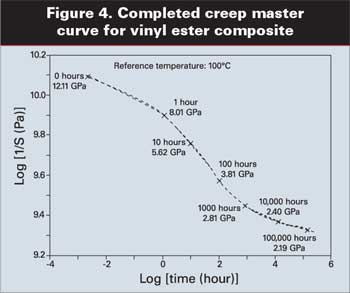
Очевидно, что материал совсем жесткий при 100°C при  исходном модуле в 12.11 ГПa (более 1.75 миллионов фунтов на кв. дюйм). Но после 10 часов под нагрузкой кажущийся модуль упругости понизился примерно на 50%. Возвращаясь к нашему уравнению, которое определяет соотношение кажущегося модуля упругости и деформации, можно заметить, что снижение  кажущегося модуля упругости на 50% равно увеличению общей деформации вдвое. Иными словами, в этой точке деформация упругости примерно равна начальной деформации.

После 1000 часов (через шесть недель), Ea уменьшилась на чуть больше, чем 75%. Это означает, что общая деформация теперь в четыре раза больше, чем начальная деформация. Спустя 10,000 часов (через 14 месяцев), она уже в пять раз больше. Такое поведение может быть смоделировано для любого набора условий.

Напряжение

Мы уже дали разъяснения по двум или трем факторам в нашей модели. Теперь все, что нам осталось сделать, это определить напряжение. Как только мы определим напряжение, мы сможем преобразовать расчет кажущегося модуля в расчет деформации. Так, например, если мы прикладываем напряжение в 12.1 МПa (1755 фунтов на кв. дюйм), мы получим начальное напряжение в 0.1%. Через 10 часов оно повысится до 0.2%. Через 1000 часов это будет уже 0.4%, а через 10,000 часов это будет уже 0.5%.

Нам известно, что у всех материалов имеется лимитирующая деформация, за пределами которой они либо становятся текучими, либо разрушаются. В случае использования очень жесткого материала, такого как композит со стекловолокном, характер разрушения будет хрупким, и избыточная деформация приведет к растрескиванию. Если бы пластмассовые материалы были идеально эластичными, все, что нам понадобилось бы сделать, так это просто измерить предельную деформацию, и мы смогли бы легко рассчитать ожидаемое время до  отказа для каждого данного напряжения. Следует избегать напряжений, которые могут вызывать прогнозируемые отказы до истечения желательного срока эксплуатации продукта.

К сожалению, у пластмассовых материалов не бывает идеально эластичного поведения на протяжении всей кривой «напряжения – деформации». Как мы продемонстрировали в части, опубликованной в прошлом месяце, линейно упругое поведение, можно получить для сравнительно небольшой части кривой «напряжения – деформации» до точки, известной как предел упругой деформации. (Заметим вскользь, что предел упругой деформации материала это параметр, который очень полезно иметь в перечне данных. Но не стоит надрываться, отыскивая эти данные, поставщики материалов их не предоставляют).

После того, как напряжения достаточно высоки для того, чтобы превысить предел упругой деформации, применение следующего приращения напряжения приводит к деформации большей, нежели можно ожидать при идеальном эластичном поведении. По этой причине нам необходимо иметь кривую «напряжения – деформации» для материала. И нам не может быть достаточно кривой «напряжения – деформации» при комнатной температуре; она должна быть сгенерирована при той же температуре, что и та, которую мы используем для моделирования поведения ползучести. До тех пор, пока прогнозируемая обобщенная кривая деформации от ползучести будет оставаться на уровне или ниже предела упругой деформации, мы можем использовать данные, вычисленные непосредственно из уравнения для Ea. Как только прогнозируемая деформация превысит предел упругой деформации, мы должны будет внести коррективы в расчет, эмпирически используя реальные значения с кривой «напряжения – деформации».

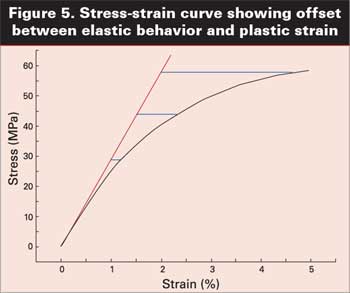
На Рисунке 5 представлен пример этого перехода от прогнозируемого линейного поведения к реальному отклику. Это кривая «напряжения – деформации» при комнатной температуре для ненаполненного ацеталевого сополимера, но принцип один и тот же для любого материала. Линия модуля показывает отклонение кривой от идеально упругого поведения (красная линии). По мере того, как прогнозируемая деформация с обобщенной кривой становится все больше, поправочный коэффициент становится больше, поскольку материал отклоняется от линейного поведения под все более возрастающим углом. При прогнозируемой 1% деформации реальная деформация составляет примерно 1.2%. Но при прогнозируемой деформации в 1.5% реальная деформация составляет примерно 2.3%. А при прогнозируемой деформации в 2% реальная деформация будет в два раза выше прогнозируемой при 4.65%.

У нас есть технология

Итак, мы рассмотрели все три фактора, которые определяют поведение ползучести материала: температуру, время и напряжение. Используя эти инструменты, мы можем дать ответы на трудные вопросы о поведении материала при практически любых условиях постоянных нагрузок, которые только можно вообразить, и это можно осуществлять в пределах разумных временных рамок всего за небольшую часть затрат на испытания в режиме реального времени.

В нашем последнем выпуске мы проиллюстрируем использование этих инструментов при выборе материала для двух применений, используемых на очень различных рынках. В одном случае анализ позволил избежать использования материала, который был дешевле, но вызвал бы отказ. В другом случае анализ показал, что можно использовать материал, который обходится дешевле, чем изначально выбранный для этого применения.

Newchemistry.ru