Энергетика: прыжок в сторону
Современная энергетика базируется на машинах, преобразующих разность тепловых потенциалов в другие виды энергии, причем это преобразование далеко не полное.

Всем известна предельная формула Карно для идеальной тепловой машины. Считается, что эта формула предсказывает максимально возможный КПД для тепловой машины и неявно содержит в себе закон роста энтропии – второе начало термодинамики. В основном проблема повышения КПД в энергетике решается в лоб - путем повышения температуры рабочего тела. Известны успешные попытки решения этой проблемы иначе, пример - водоаммиачный термодинамический цикл Калины. Цель этой статьи указать еще два способа повышения КПД термодинамического цикла тепловой машины. Но это не лобовая атака - это прыжок в сторону, качественный и в некотором смысле "зубодробильный" для целых отраслей мировой промышленности.
Управление энтропией.
В последнее время в печати появляются сообщения о больших успехах различных исследовательских команд в области магнитокалорического и электрокалорического эффекта. Имеются сообщения о том, что порошки соединений гадолиния под воздействием внешнего магнитного поля разогреваются на 12 градусов, а при снятии внешнего магнитного поля охлаждаются на эту же величину. Имеются сообщения о том, что приблизительно такого же по величине теплового эффекта можно достичь и воздействием относительно небольшого по напряженности внешнего электрического поля на пленки некоторых веществ. Не вызывает сомнений, что наиболее подходящие вещества, то есть вещества с максимальным магнитокалорическим или электрокалорическим эффектом, могут быть использоваться в виде мелкодисперсных механических растворов, а жидкость тут может выступать простым механическим носителем для порошка. Использование жидкостей как носителей для механических растворов позволит легко использовать порошки в теплообменниках и рекуператорах, легко вводить порошки в зоны воздействия внешнего поля и так же легко выводить эти порошки из под воздействия внешних полей. Кроме того, даже обычные жидкие растворы имеют кристаллоподобную структуру, так как при растворении происходит сольватация молекул или ионов растворяемого вещества, некоторая молекулярная упорядоченность возникает и при образовании мицелл. Это означает, что существуют интересные перспективы в смысле использования в энергетике возможных тепловых эффектов возникающих под воздействием внешних полей на обычные и коллоидные растворы. Внешние поля должны упорядочивать молекулярную и квантовую структуру растворов, тем самым уменьшать хаотичность в растворе, а значит, уменьшая энтропию. Следовательно, при воздействии внешнего поля на раствор он должен нагреваться, при снятии такого воздействия раствор будет терять упорядоченность и остывать, его энтропия будет возрастать. Итак, для примера, можно предложить очевидную простейшую схему рекуперации на основе электрокалорического эффекта.
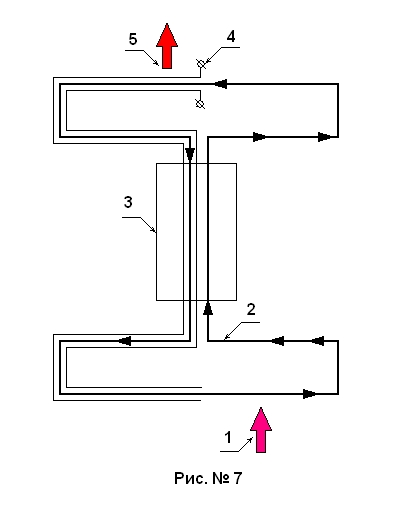
См. рисунок № 7.
На рисунке № 7 показан замкнутый контур, в котором циркулирует механический раствор вещества способного к сильному электрокалорическому эффекту. В контуре осуществляется циркуляция раствора между верхним и нижним температурными уровнями находящимися в верхней и нижней части рисунка соответственно. Цифра 4 указывает на клеммы пары проводящих контуров, эти два контура, обхватывающие поток раствора, формируют электрическое поле, воздействующее на порошок упомянутого вещества. Горячий раствор подают между контурами 4 где под воздействием электрического поля происходит изменение его термодинамического состояния, в результате чего раствор нагревается, выделившееся высокотемпературное тепло отводится по назначению, например, передается в нагреватель тепловой машины. Этот отвод тепла указан на рисунке стрелкой 5 . После того, как температура раствора несколько уменьшится в результате теплоотдачи, его подают в теплообменник 3 , при этом воздействие внешнего поля на раствор не прекращается. После того как температура раствора в теплообменнике понизится до температуры близкой к температуре нижнего температурного уровня, раствор выводят из под воздействия внешнего поля, в результате чего происходит возвращение к нормальному термодинамическому состоянию, температура раствора понижается, в результате к холодному раствору становится возможным подвести низкотемпературное тепло, обозначенное стрелкой 1 . Это низкотемпературное тепло может отводиться от холодильника тепловой машины или изыматься от внешнего источника низкотемпературного тепла. Затем низкотемпературный раствора подают в теплообменник 3 где происходит его нагревание то температуры близкой к температуре верхнего температурного уровня.
Обратим внимание на то, что эффективность такого теплового насоса необычайно высока и не определяется пределом Карно. Говоря прямо, на базе такого теплового насоса может быть построен двигатель добывющий энергию путем охлаждения окружающего воздуха. Нефть, уголь, газ будут исключены из энергетики. Это первый прыжок в сторону. Но и это еще не все, есть шанс прыгнуть еще дальше.
Растворы.
Для пояснения сути дела возьмем, для начала, некое растворимое вещество и некий растворитель. Пусть это вещество растворяется в упомянутом растворителе с поглощением тепла и соответственно его растворимость растет с ростом температуры. Будем полагать, для простоты, что суммарный объем вещества в процессе растворения остается неизменным. Нас будут интересовать насыщенные растворы, то есть такие, в которых растворение данного вещества при фиксированной температуре уже невозможно. Особо акцентируем внимание на том факте, что насыщенный раствор это система, находящаяся в динамическом равновесии, т.е. постоянно часть молекул раствора переходит в исходное нерастворенное вещество и в это же время равная часть вещества растворяется.
Процесс растворения во многом подобен процессу фазового перехода, такому как испарение воды, однако имеет ряд особенностей, мы упомянем о них ниже и вкратце. Фазовый переход и растворение описываются в классической термодинамике одинаково. Движущей силой растворения, равно как и испарения принято считать различие в энергии Гиббса вещества в конкретных фазах. Если жидкость интенсивно кипит или вещество интенсивно растворяется, раствор не насыщен, значит имеется разница между энергией Гиббса пара и энергией Гиббса воды, для раствора это будет разница между энергией Гиббса раствора и энергией Гиббса растворимого вещества. Теперь присмотримся к растворам пристальнее. В первую очередь упомянем, что растворы характеризуются наличием осмотического давления, вычисляемого по газовым законам и исследованного Вант-Гоффом. Posm = RT/V, где Posm – осмотическое давление, R – газовая постоянная, T – температура, V – объем раствора. Если поместить растворимое вещество в растворитель, то изначально никакого раствора существовать не будет, следовательно, не будет существовать и никакого осмотического давления для данного раствора. Затем в процессе растворения будет формироваться раствор все большей и большей концентрации, соответственно будет возрастать осмотическое давление в растворе. Поскольку в нашем случае (а именно этот случай нам интересн) растворение будет сопровождаться поглощением тепла из окружающей среды в изотермическом режиме, то из общепринятых соображений, можно говорить о том, что энтропия системы, состоящей из растворимого и растворителя, возрастает. После достижения насыщения величина осмотического давления раствора будет максимальной. При таком растворении никакая внешняя работа системой совершена не будет, ибо объем системы состоящей из растворимого и растворителя остался неизменным. Вся наличная энергия Гиббса реализуется как осмотическое давление раствора. Рассмотрим рисунок № 1
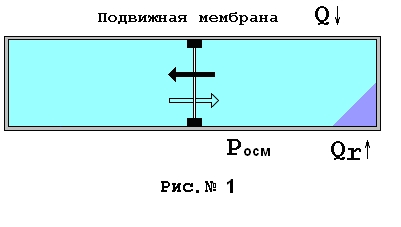
Здесь изображен сосуд, ограничивающий объем растворителя и растворимого вещества. Имеется подвижная идеальная мембрана, пропускающая только растворитель и движущаяся без трения. Растворим вещество еще раз справа от мембраны, процесс будем поддерживать изотермическим. Как только возникнет осмотическое давление с правой стороны, мембрана начнет двигаться влево, пропуская воду направо. Передвигаясь, мембрана дойдет до левой стенки сосуда. Никакой работы на мембране совершено не будет, так как двигать мембрану может бесконечно малое избыточное давление справа, возникающее под действием осмоса. В результате мембрана дойдет до левой стенки, когда концентрация раствора справа будет еще минимальной. И только позже, когда раствор станет насыщенным, весь объем сосуда будет занимать раствор с фиксированной концентрацией, вот после этого ничего уже происходить не будет. В этом виде вся система в целом будет обладать неким термодинамическим состоянием, характеризующимся набором термодинамических величин, температурой, объемом, концентрацией, давлением, осмотическим давлением, энтальпией. Подчеркнем, что достигнутое конкретное состояние системы характеризуется единственной конкретной величиной поглощенной в процессе растворения теплоты - Qr.
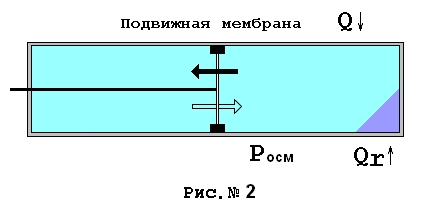
Снабдим теперь нашу подвижную мембрану штоком. При тех же условиях еще раз проведем процесс растворения. Однако теперь будем поддерживать концентрацию справа от мембраны на уровне насыщенного раствора для того, чтобы осмотическое давление справа было максимальным. При помощи штока будем снимать полезную работу, позволяя мембране медленно двигаться влево до упора. Итак, вся наличная энергия Гиббса будет расходоваться на создание осмотического давления, следовательно, теплоты растворения Qr уже не хватит на совершение системой полезной работы на штоке DA= Posm * DV. Система вынуждена будет принять дополнительное тепло и трансформировать его в работу DQ= DA= Posm * DV. Исходя из канонов термодинамики, следовало бы ожидать, что при совершении работы система будет иметь в конечном состоянии большую энтропию, нежели в случае, когда она не совершала бы полезной работы. Причина такого предположения в том, что система во втором случае приняла извне тепла больше ровно на величину необходимую для совершения работы на штоке. Однако конечное состояние и в первом и во втором случае будут иметь одни и те же параметры: тот же объем, та же температура, то же давление системы в целом и осмотическое давление раствора, ту же концентрацию- концентрацию насыщения. Очевидно, ничего не изменится, если мы будем позволять поршню двигаться при любом осмотическом давлении, меньшем, чем осмотическое давление насыщенного раствора. Принять любой уровень давления на поршень нам позволяет конечная скорость диффузии в растворителе молекул, ионов или неких ассоциаций растворимого вещества. Как известно скорость диффузии зависит от температуры, поэтому мы можем позволять поршню сдвигаться при некотором, устраивающем нас усилии. То есть конечное состояние системы будет тем же не зависимо от того, какую работу совершила система, и сколько тепла для этого было дополнительно принято извне. Интересно, не правда ли?
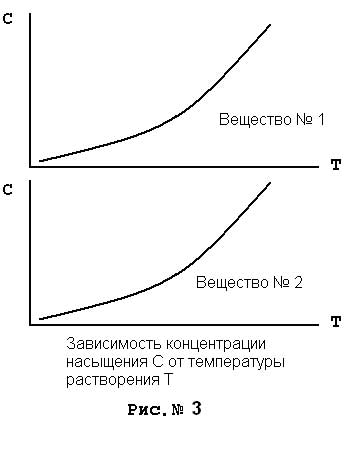
Рассмотрим еще более интересный случай. Пусть имеется некое другое растворимое вещество, причем такое, что его термодинамические параметры полностью идентичны растворимому веществу, рассмотренному ранее, будем называть его вещество № 2. Пусть параметры его растворимости будут те же что и у вещества № 1. Та же теплота растворения в одинаковом диапазоне температур, а значит энергия Гиббса и ее изменения при растворении, та же теплоемкость веществ и их растворов и т.п. Кривые растворимости одинаковы. См. рисунок № 3
Одним словом, вещество №2 будем считать полностью идентичным веществу № 1 за исключением одной небольшой детали – пусть вещество № 2 образует в этом же растворителе не обычный, а коллоидный раствор. Особенность коллоидных растворов состоит в том, что львиная доля наличной энергии Гиббса при их образовании тратится на создание очень большой поверхности микрокапелек раствора – мицелл. Соответственно осмотическое давление, создаваемое насыщенным коллоидным раствором вещества № 2 может быть многократно меньше осмотического давления раствора вещества № 1, так как в этом случае осмотическое давление будет создаваться не молекулами и ионами, а мицеллами, включающими в себя некоторое количество молекул. В теории растворов принято для учета численного отклонения осмотического раствора от формулы Вант-Гоффа вводить в нее экспериментальный коэффициент - i, получивший название изотонического коэффициента. Итак, для раствора вещества № 2. формула Вант Гоффа будет выглядеть так Posm = iRT/V, причем i для вещества № 2 будет существенно меньше единицы.
Все приведенные ранее рассуждения для рассмотренных выше случаев растворения со снятием работы на штоке и без снятия работы сохраняют свою силу применительно и к коллоидному раствору. Отличие будет состоять лишь в том, что с помощью коллоидного раствора можно будет получить меньше полезной работы на штоке и конечно система поглотит от внешнего нагревателя меньшее количество дополнительного тепла необходимого для совершения этой работы. Посмотрим теперь на рисунок № 4.
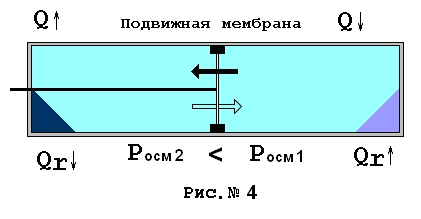
Пусть слева находится раствор вещества № 2 и его коллодиный раствор, справа вещество № 1 и его раствор, это обычный раствор. Пусть имеется некий запас нерастворенного вещества первого и второго типа справа и слева. Пусть изначально подвижная мембрана жестко зафиксирована стопорами, так как показано на рисунке. Пусть емкость полностью изолирована от окружающей среды. Итак, энтальпия масс веществ слева и справа, их потенциалы Гиббса абсолютно одинаковы, но осмотические давления растворов различны. Посмотрим, что произойдет, если убрать стопоры. Под действием большего осмотического давления справа мембрана начнет двигаться влево. Равновесие насыщенного коллоидного раствора слева будет нарушено, так как растворитель начнет перетекать через мембрану направо.Заметим особо, энергия затраченная на образование поверхности мицелл носит потенциальный характер и полностью обратима, следовательно самопроизвольно возвращается при уменьшении объема раствора. В результате в левой части емкости из раствора начнет выделяться вещество № 2. Все выделенное в этом процессе тепло будет равно тепловому эффекту растворения этого вещества, плюс тепло численно равное работе избытка осмотического давления обычного раствора справа DA=DPosm * DV, здесь DPosm = Posm1 - Posm2. По мере продвижения мембраны влево направо будут поступать порции чистого растворителя. Это даст возможность растворяться веществу № 1 справа и доводить концентрацию до насыщенного состояния, на это потребуется тепло в точности равное теплу возникающему в результате выделения из раствора вещества № 2. Кроме того, для совершения работы на мембране потребуется дополнительное тепло, в точности равное теплу, выделившемуся от этой же работы на другой стороне. В конечном счете, когда мембрана дойдет влево до упора все вещество № 2 выделится из раствора слева от мембраны, справа от мембраны будет находиться насыщенный раствор вещества № 1 перетянувшего на свою сторону весь растворитель. При этом ни объем, ни давление, ни температура, системы в целом не изменится, так как растворитель целиком уйдет в раствор № 1. Можно сделать вывод – энтропия системы в целом до начала процесса и после его окончания останется неизменной. Такой вывод следует из энергетической идентичности растворов и растворимых веществ по ранее определенным условиям и из отсутствия теплообмена с окружающей средой.
Конечно реальная картина динамики изменения состояния растворов и движения мембраны, будет несколько иной, температуры правой и левой частей, их осмотические давления и концентрации, могут отличаться от предложенного описания. Реальная динамика зависит от множества факторов, теплопроводности веществ, раствора, свойств мембраны и т.п. Но для нас важно то, что при любой динамике в теплоизолированной системе конечное состояние системы будет характеризоваться не изменившейся относительно начального момента температурой, абсолютным давлением, объемом и следовательно энтропией. Теперь нам останется только снабдить рассмотренную изолированную систему штоком для того, чтобы снимать работу dA=DPosm * dV. Когда мы начнем снимать работу на штоке, произойдет перетекание части имеющейся внутренней энергии теплоизолированной системы в полезную работу, ибо энергию для совершения работы система извне взять не может по условию ее теплоизоляции от окружающей среды. Конечно, температура системы к концу хода поршня упадет, изменится насыщенная концентрация раствора вещества № 1, она станет меньше, разница осмотического давления Posm по ходу движения мембраны тоже будет падать по мере падения общей температуры системы, но объем и абсолютное давление после окончания процесса останутся неизменными. Возникает законный вопрос: что принципиально изменяется, ведь мембрану следует вернуть в изначальное состояние, а значит приложить для этого всю полученную работу? Все верно, но возвращать систему в исходное состояние следует при пониженной температуре. Для этого ее следует охладить, отведя тепло некоему телу, вся хитрость в том какому именно, об этом ниже. Очевидно, что в процессе охлаждения системы из раствора будет выделяться вещество № 1, так как нарушиться равновесие раствора теперь уже из-за изменения температуры. Выделение из раствора вещества №1 будет сопровождаться выделением тепла, которое тоже следует отвести. После того как требуемая температура будет достигнута, можно вернуть мембрану в исходное положение. При этом работы будет затрачено существенно меньше и соответственно количество тепла, которое необходимо будет отвести в окружающую среду - уменьшается.
Итак, рассмотрим термодинамику идеальной осмотической – обратноосмотической машины. Для начала оценим КПД такой машины, а позже представим схему ее работы по замкнутому циклу. На рисунке показана сборка, состоящая из цилиндра снабженного подвижным поршнем, мембрана которого способна пропускать только растворитель. Поршень разделяет емкость на две части, в которых находятся вещества и их растворы. Пусть тепло как от внешнего нагревателя, так и между частями цилиндра передается мгновенно, термодинамический процесс при движении поршня изотермический, растворы находятся все время в состоянии насыщения. См. рисунок № 5. Начальное положение поршня – крайнее правое.
Нам уже ясно, что теплоты растворения для обоих веществ - Qr одинаковы, а потому полностью компенсируются. Однако, раствор вещества №1 совершает работу и для этого ему требуется дополнительное тепло Q1. Над раствором вещества №2 совершается работа и для сохранения неизменной его температуры требуется отвести тепло Q2. Для вещества №1 количество внешнего тепла DQ1 = P*DV , для вещества № 2 количество отведенного наружу тепла DQ2 = i*P*DV. Но поскольку мы располагаем неким, не важно, каким именно, механизмом передачи тепла из левой части цилиндра в правую, количество тепла, которое следует подвести к раствору веществу № 2 извне, составит DQv =DQ1 - DQ2 и DQv * = P* (1-i)*DV.
Получим идеальный КПД машины, использующий прямой и обратный осмос.
A = Qvmax-Qvmin
K= (Qvmax-Qvmin)/ Qvmax.
Раскрывая выражение для КПД, получим:
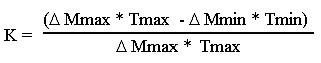
или иначе
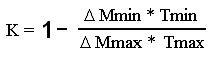
Где:
DMmax – растворимость при максимальной температуре цикла Tmax.
DMmin – растворимость при минимальной температуре цикла Tmin.
Очевидно, что этот КПД существенно выше КПД идеального цикла Карно, так как отношение DMmin/DMmax может находится в диапазоне (0.8 – 0.1) и зависит от конкретных веществ и температурного диапазона. Сравните с КПД Карно.
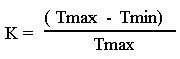
Было бы интересно оценить, как изменится энтропия в системе, состоящей из рассматриваемой машины и классического нагревателя и холодильника. Достаточно очевидно, что в процессе работы этой машины энтропия убывает DS = (1-i)* R* (DMmin - DMmax). Вывод этой формулы нет необходимости приводить в силу его очевидности, так как DQ = (1-i)* DM*RT, а DS = DQ/T.
Рассмотрим теперь вопрос сохранения тепловой энергии в процессе охлаждения цилиндра.
Вообще говоря, можно представить себе некий закольцованный конвейер из микроцилиндров, обменивающихся теплом. Пусть мембраны в микроцилиндрах неким способом обездвиживаются в процессе нагрева – охлаждения и отпускаются только в крайних температурных точках, где и совершается работа силами осмотического давления или против этих сил. Поскольку теплоты растворения и теплоемкости содержимого цилиндров равны, а работа в процессе нагрева или охлаждения не совершается, то в теплообмене на встречных потоках состоящих из микроцилиндров потери тепла отсутствуют и цикл замыкается. То есть, из-за принятой полной энергетической идентичности растворов никакого дисбаланса в процессе теплообмена между цилиндрами не возникает, говоря иначе, соблюдается баланс по энтальпиям. Но можно предложить более технически реалистичные концепции. На рис. № 6 представлен один из возможных вариантов.
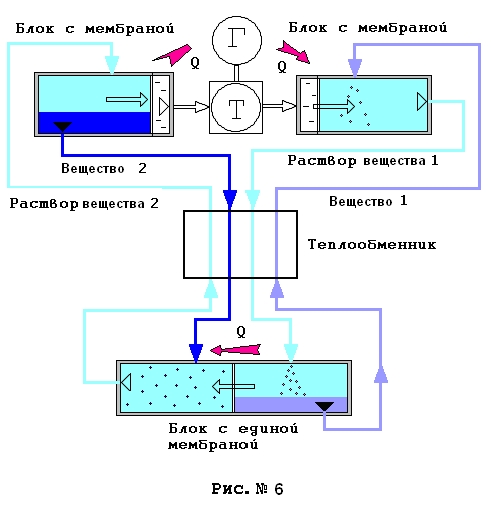
Справа вверху показана емкость с мембраной, в которой растворяется вещество № 1 и в которую слева приходит растворитель из полости с чистым растворителем, где его давление минимально. Растворитель поступает сквозь полупроницаемую мембрану. На схеме это перемещение растворителя обозначено прозрачной стрелкой. Раствор вещества № 1 тут создает максимальное осмотическое и гидравлическое давление во всей системе. К этой емкости подводится как тепло как извне, так и от емкости, где выделяется из раствора вещество № 2, что обозначено стрелками и значком Q. Далее насыщенный раствор вещества № 1 подается в теплообменник, где он остывает, и часть вещества выделяется из раствора по причине температурного нарушения равновесия раствора. Холодный насыщенный раствор вещества № 1 вместе с кристаллами этого же вещества попадает в правую часть блока с единой мембраной. Это холодный блок, здесь температура цикла минимальна. Поскольку гидравлическое давление в этой емкости равно давлению в горячем блоке, а осмотическое намного ниже, растворитель переходит в левую часть холодного блока с диной мембраной как это показано прозрачной стрелкой. Вещество № 1 при этом выделается из раствора, а тепло кристаллизации передается в левую половину блока с единой мембраной и частично сбрасывается наружу. Затем вещество № 1 через теплообменник, проходя который она нагревается, подается в горячий блок с мембраной. Поскольку оба рассмотренных потока идущих через теплообменник перемещаются между емкостями с одинаковым гидравлическим давлением, то работой на это перемещение мы в рассматриваемом идеальном случае пренебрегаем из-за ее очевидной малости.
Вернемся теперь к холодной части цикла. Итак, растворитель перемещается из правой в левую из частей холодного блока с единой мембраной. Гидравлическое давление тут меньше чем в правой части, однако, некоторое повышение гидравлического давления создается за счет осмотического давления растворяющейся в режиме насыщения вещества № 2. Растворение вещества № 2 требует некоторого количества тепла, которое поставляет выделяющееся из раствора справа вещество № 1. Далее насыщенный раствор вещества № 2 с необходимым количеством кристаллов вещества № 2 подается в теплообменник, где раствор нагревается, и все идущие вместе с раствором вещества № 2 кристаллы растворяются. Тепловые эффекты растворения вещества № 2 и выделения вещества № 1 из раствора в теплообменнике равны, равны теплоемкости и массы веществ и растворов, поэтому тепловой баланс в теплообменнике соблюдается и равен нулю. Вообще говоря, теплообменник этой машины играет роль своеобразного теплового затвора, поэтому желательно, чтобы он был как можно более совершенным. Далее в горячем блоке с мембраной из - за перепада гидравлических давлений происходит перетекание растворителя в часть емкости занятой чистым растворителем. Это перетекание происходит против сил осмотического давления, поэтому давление растворителя в емкости с чистым растворителем меньше чем давление раствора, но все еще достаточно велико. Нарушение равновесия раствора приводит к выделению вещества № 2, что сопровождается выделением тепла, которое утилизируется растворяющимся веществом № 1. Полученный при некотором, достаточно большом давлении, чистый растворитель подается на вход гидротурбины, приводящей в действие генератор. Далее растворитель при минимальном давлении подается в предмембранную полость блока, где растворяется вещество № 1. Так образуется замкнутый термодинамический цикл, КПД которого выше «предельного» КПД Карно. Конечно, вещество будет стремиться к диффузии вдоль труб теплообменника, но скорость диффузии мала по сравнению со скоростью движения жидкостей, а потому этим фактором можно пренебречь.
Можно показать, что подобного рода машина может быть создана и для веществ линии, растворимости которых не обязательно совпадают точно. Кроме того, можно доказать, что не обязательно использовать вещества, образующие именно коллоидные растворы.
Технические характеристики
Машины на основе осмотических технологий не будут компактными и легкими, потребуется большая площадь мембран, хотя, мембраны следует укладывать как можно более компактно. Конструкции должны будут выдерживать большие давления, это значит, они будут толстостенными, потребуется хорошая теплоизоляция. Будет необходим специальный блок очистки, поддерживающий растворитель чистым, так как все мембраны будут в той или иной степени проницаемы для растворимых веществ. Все это означает, что такая машина будет иметь очень большой вес, приходящийся на единицу вырабатываемой мощности. Возможно, такую энергоустановку можно будет разместить на торговом судне и конечно в стационарном наземном виде. Навряд ли удастся добиться полной энергетической идентичности растворов, хотя к этому не может быть никаких принципиальных препятствий. Однако все эти недостатки машин сторицей окупятся при нынешних сверхвысоких ценах на энергоносители.
Вывод
Есть все основания полагать, что тандем из осмотической машины и теплового насоса способен создать двигатель с предельным идеальным КПД в 100%. Появляется теоретическая возможность построить двигатель, не нуждающийся в высокотемпературном источнике тепла и низкотемпературном холодильнике. И это будет скачком в сторону от традиционного пути в энергетике
Пелипенко А.И инженер
Колисниченко Н.Д инженер.