В статье представлено научное обоснование технического решения по транспортировке жидкости (газа) в трубопроводах за счет энергии самой жидкости. По просьбе автора сохранен оригинальный (научный) стиль изложения материала.

В 1938 году П. Л. Капица открыл (а Л. Д. Ландау через три года научно обосновал) явление сверхтекучести квантовой жидкости. Согласно открытию, квантовая жидкость способна не только протекать через тончайшие капилляры без сопротивления, но и самостоятельно подниматься по ним, вопреки явлению гравитации. Ландау объяснял эту способность наличием в квантовой жидкости сверхтекучей компоненты. При этом сверхтекучесть проявляется лишь в том случае, когда сверхтекучая компонента преобладает над нормальной.

Говоря о нормальной и сверхтекучей компоненте, необходимо иметь в виду, что речь идет об исключительно разных видах движения:
«Следует, однако, самым решительным образом подчеркнуть, что рассмотрение жидкости как смеси нормальной и сверхтекучей ее частей является не более чем способом наглядного описания явлений, происходящих в квантовых жидкостях... В действительности надо говорить, что в квантовой жидкости может существовать одновременно два движения, каждое из которых связано со своей эффективной массой (так что сумма обеих этих масс равна полной истинной массе жидкости)»/Л. Д. Ландау, Е. М. Лифшиц, «Гидродинамика»/.

Для объяснения сверхтекучести Ландау использовал аналогию с твердым телом. В естественном же ряде состояний остался пробел – нормальная вязкая жидкость, к которой относятся и газ, и вода, и нефть. Для придания нормальной жидкости сверхтекучих свойств необходимо создание в ней сверхтекучей компоненты. По своей сути сверхтекучая компонента – не что иное, как вращательное движение жидкости, ротон (от лат. roto – вращаюсь, верчусь). В теории сверхтекучести ротон – элементарное возбуждение (квазичастица).

«Подчеркиваем, что хотя мы говорим здесь о «частице», но ее «элементарность» нигде не используется. Поэтому полученные формулы в равной степени применимы и к любому сложному телу, состоящему из многих частиц…»
/Л. Д. Ландау, Е. М. Лифшиц, «Теория поля»/.

Создание в жидкости сверхтекучей компоненты – вращательного движения – задача элементарная.

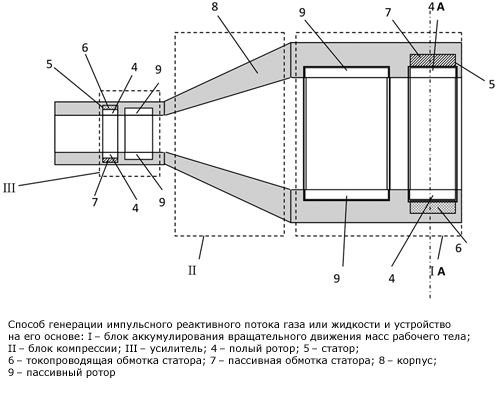
На рисунке представлена принципиальная схема «устройства для генерирования реактивного импульсного потока газа или жидкости». (Такое название устройства обусловлено его двойным назначением. В трубопроводах нет необходимости получать реактивный поток – в общепринятом понимании, относящемся к двигателям).

На токопроводящую обмотку статора блока аккумулирования подается электрический импульсный ток, фиксированный по величине и продолжительности и переменный по частоте. Для этого используется частотно-импульсный преобразователь. Разгоняется ротор равноускоренно, для чего частота тока возрастает пропорционально росту собственной частоты вращения ротора. Присоединение масс транспортируемой жидкости может происходить только при переменном (ускоренном) движении. Причем движение должно быть равноускоренным с небольшой фиксированной величиной ускорения. Только соблюдение этого условия дает возможность формирования устойчивого состояния рабочего тела и постоянной его энергии состояния.

«Изменение состояния (или положения) одной из частиц приводит к изменению создаваемого ею поля, которое отражается на другой частице лишь через конечный промежуток времени, необходимый для распространения этого изменения до частицы»/БСЭ, статья «Поля физические»/.

Полученное состояние представляет собой вихревую трубку. Энергия состояния жидкости в вихревой трубке является функцией собственной угловой скорости, а также внутренней энергии и плотности, которые, в свою очередь, являются функцией собственной угловой скорости. Вывод: величина собственной угловой скорости определяет физическое состояние жидкости.

Описывая свободное вращательное движение, Л. Ландау подчеркивает его обязательную потенциальность, выражаемую равенством rot vs = 0, «которое должно иметь место в любой момент времени во всем объеме жидкости». Потенциальность означает, что при «вращательном движении» не совершается работа. Поэтому движение – не процесс, а состояние. И поэтому давление жидкости на стенки сосуда практически равно нулю.

Фактически давление зависит от соотношения величин вращательного движения и поступательного перемещения жидкости, которое в рассмотренном состоянии отсутствует.

Вообще же аккумулирующее свойство вращательного движения известно с древности. Аккумулируется именно движение. А массы, вовлеченные во вращательное движение, являются присоединенными и по своей сути вторичны.

Рассмотренное состояние является устойчивым (атом, космос). В предлагаемом решении его можно считать квази-устойчивым.

Особое значение в вихревой теории имеют теоремы Гельмгольца, которые Пуанкаре считал наиболее значительным вкладом в гидродинамику. Их сутью является закон «вмороженности вихревых линий», позволяющий рассматривать «вихревые образования» как некоторые «материальные объекты, подобные массам в классической механике». При этом «перемещение вращающихся масс всегда перпендикулярно их плоскости вращения». В трубе перемещение происходит по оси трубы, являющейся осью вращения.

Переход от чисто вращательного движения к вращательно-поступательному, винтовому, происходит под действием внешнего возбуждения на поле вращения. По своей сути этот переход представляет собой вынужденное излучение. Для понимания процесса необходимо вновь обратиться к аналогии (метод аналогий при доказательстве своих теорий использовали, кстати, и Ландау, и Эйнштейн).

«Вынужденное излучение (вынужденное испускание, индуцированное излучение) – испускание электромагнитного излучения квантовыми системами под действием внешнего (вынуждающего) излучения»/Физический энциклопедический словарь, «Вынужденное излучение»/.

Согласно постулированной Эйнштейном теории, вынужденное излучение – процесс,
обратный поглощению. Эти процессы равны при соблюдении определенного условия, касающегося критической частоты внешнего возбуждения. Критическая величина частоты внешнего возбуждения (n) определяется частотой собственных (свободных) колебаний системы и должна соответствовать условию n ≤ ω/2π. При нарушении последнего, то есть при превышении частоты внешнего возбуждения над частотой собственных колебаний, происходит разрушение поля вращения – вихревой трубки.

Способность к релаксации поля вращения, сохранение заданного состояния и его характеристик обусловлено наличием собственного спина. Это является важнейшим отличием предлагаемого способа от других известных, определяет его уникальность и эффективность.

Релаксация в данном случае есть процесс поглощения, обратный и равный по величине генерированию (испусканию). Генерируемый объем жидкости одновременно замещается равным объемом жидкости, исходное состояние которого практически соответствует состоянию жидкости в поле вращения, так как оно является частью вихревой трубки.

Фактически речь идет не о присоединенных массах, а о присоединенном вихре. Внешняя энергия расходуется не на перемещение объемов (масс) жидкости, а на поддержание заданного состояния, на поддержание равновесия системы, которое является квазиустойчивым. Перемещение же осуществляется исключительно за счет энергии состояния жидкости в вихревой трубке, представляющей сумму кинетической и внутренней энергий жидкости.

Производительность системы при этом определяется исключительно энергией состояния системы. Полученное состояние поля вращения присоединенных масс уникально. Оно одновременно является и устойчивым, и возбужденным. И устойчивость, и возбужденность являются функцией одной величины – угловой скорости. Последняя определяет и линейную скорость перемещения жидкости по трубе.

К сожалению, статистические данные об этом процессе пока отсутствуют. Но для расчета производительности мы можем обратиться к теории и аналогии.

Уже говорилось, что каждая компонента движения связана со своей эффективной массой. В рассматриваемом состоянии присутствует только вращательное движение, эффективную массу которого, по аналогии с квантовой жидкостью, можно принять равной ≈ 3,08 m0 / Физический энциклопедический словарь, статья «Эффективная масса»/.

Это соответствует и логической модели, где плотность жидкости в кольце тора значительно выше ее нормальной плотности. Но объем, занимаемый жидкостью, – это лишь малая часть объема трубы. Скорость линейного перемещения жидкости определяется на основе представления, что движение является сложным, винтовым. Учитывая ничтожность величины диаметра трубы относительно линейной скорости вращения, можно считать, что
v ≈ vs ≈ aω, где v – линейная скорость перемещения жидкости по оси трубы.

С появлением линейного перемещения жидкости появляется нормальная компонента движения, что отрицательно влияет на текучесть жидкости. Для снижения этого влияния необходимо снизить период действия внешнего возбуждения до допустимого минимума, а объемы перемещения регулировать частотой внешнего возбуждения. Теперь можно вывести формулу плотности потока жидкости (Р) в трубе: Р ≈ mэ vsпτ или Р ≈ ρVaωпτ, где п (1/с) – частота внешнего возбуждения в единицу времени (→ max); τ(с) – период (продолжительность) действия внешнего возбуждения. Величина mэ vsτ ≈ ρVaωτ является величиной единичного импульса (р), тогда Р = рп. Объем единичного импульса определяется объемом полости ротора в зоне генерирования и собственной угловой скоростью и представляет, по аналогии, «квазичастицу» конкретного поля.

Величина импульса внешнего возбуждения, обеспечивающая ускоренное вращение ротора до достижения заданной величины угловой скорости (частоты собственных колебаний), определяется по принципу «минимальной достаточности» и полностью зависит от характеристик конструкции устройства и транспортируемой жидкости, в частности – ее числа Re. Величина внешнего возбуждения генерирования потока не должна превышать величину «разгонного» возбуждения.

Частота собственных (свободных) колебаний системы (частота вращения ротора) определяет эффективность ее работы. …В среде конечного объема могут происходить свободные колебания лишь с вполне определенными частотами... Конкретные значения собственных частот зависят от формы и размеров сосуда. В каждом данном случае существует бесконечный ряд возрастающих собственных частот. Нахождение их требует конкретного исследования уравнения движения с соответствующими граничными условиями»/Л. Д. Ландау, Е. М. Лифшиц, «Гидродинамика»/. Речь идет о множественности собственных энергетических уровней системы.

Реализация представленного способа позволит, по приближенным расчетам автора, повысить пропускную способность существующих и проектируемых трубопроводов как минимум в десятки раз, значительно снизив при этом капитальные, эксплуатационные и энергетические затраты.

Представленная информация защищена патентами РФ.

Владимир ФЕДОРОВ
Энергетика и промышленность России